![]() Inhaltsverzeichnis
Inhaltsverzeichnis
![]() Einleitung, Zielstellung und Modellierung
Einleitung, Zielstellung und Modellierung
Basierend auf diesem Modell läßt sich ein einfacher Algorithmus aufstellen:
1. für alle Gelenkmengen der richtigen Mächtigkeit
2. {wenn die Gelenkanzahlen aller zu prüfenden Substrukturen die jeweilige Ungleichung erfüllen
3. {wenn die Gelenkmenge in allen Permutationen der Glieder (außer Gestell und Antrieb, sofern vorhanden) verschieden zu denen aller bereits gefundener Typen ist
4. {weiterer Typ gefunden}}}
Dieser Algorithmus löst die Aufgabe bereits vollständig. Zeile 1 stellt die Erfüllung der zweiten Forderung sicher, Zeile 3 die der dritten. Die Korrekteit wird durch die Kombination der ersten beiden Zeilen gewährleistet. In der Praxis entsteht jedoch noch eine vierte Forderung: der Algorithmus muß eine gewisse Effizienz aufweisen, um auf einer realen Maschine ablaufen zu können - das gilt sowohl für den Speicherplatz als auch für die benötigte Rechenzeit.
Der Platzbedarf wird durch die zum Herausfiltern der Redundanzen notwendige Speicherung der Typen bestimmt, denn diese Informationen haben das Volumen der größten - nämlich exponentieller - Größenordnung. Später wird sich herausstellen, daß der endgültige Algorithmus sehr zeitaufwendig und die Speicherung der Typen daher einer wiederholten Ausführung vorzuziehen ist. Der Algorithmus wird also ohnehin nur für Parameter arbeiten, für die die Hardware eine vollständige Archivierung der Typen zuläßt. Dadurch ist auch der Platzbedarf zur Laufzeit unkritisch.
Anders sieht es bei der Effizienz bezüglich der Rechenzeit T aus:
[Berechnungen zur Rechenzeit nicht übertragen]
Eine Betrachtung der Komplexität ist überflüssig: sie ist zwangsläufig exponentiell. Interessant ist daher nur der absolute Wert. Für vierzehngliedrige kinematische Ketten ergibt sich aus Tuttle's M=318.162 Typen eine Anzahl von Programschritten, die in der Größenordnung von 1040 liegt; der Initiator dieser Berechnung würde ihr Ergebnis nicht erleben. Soll der Algorithmus also jemals mit den gewünschten Parametern arbeiten, wird er entscheidende Verbesserungen erfahren müssen.
Fast jede der Strukturen, die der Basisalgorithmus durchmustert, ist unzulässig und ihre Untersuchung daher sinnlose Zeitverschwendung. So ist es naheliegend, bei der Erzeugung des Suchraumes bestimmtes Wissen über die Eigenschaften der gesuchten Objekte zu verwenden, um ihn von vornherein kleiner zu halten und so viel Aufwand für überflüssige Tests einzusparen. Natürlich müssen weiterhin alle gesuchten Strukturen im Suchraum enthalten sein, damit die zweite Forderung erfüllt bleibt. Ideal wäre ein Verfahren, das überhaupt keine unzulässigen Objekte erst erzeugt - eine besondere Überprüfung wäre dann gar nicht mehr nötig. Ein solches Verfahren ist jedoch nicht bekannt.
Zur Einschränkung des Suchraumes benutze ich lediglich die Tatsache, daß jedes Glied in einer realen Struktur mindestens zwei Gelenke besitzt. Durch diese Bedingung wird die Menge der möglichen Kombinationen von Gelenkanzahlen bei den verschiedenen Gliedern stark eingeschränkt. Diese Lösung ist recht einfach. Sicher kann man mit viel Aufwand noch mehr Rechenzeit einsparen, für die Zwecke dieser Arbeit ist das jedoch nicht erforderlich.
Das Verfahren funktioniert so, daß zuerst alle möglichen Verteilungen der Gelenke (deren Anzahl für eine bestimmte Art von Struktur ja feststeht) auf die einzelnen Glieder ermittelt werden. Für diese werden dann jeweils alle Typen ermittelt. Entscheidend für die Einschränkung des Suchraumes ist dabei, daß nur solche Gelenkverteilungen berücksichtigt werden, bei denen jedes Glied an mindestens zwei Gelenken beteiligt ist. Für die nicht vertauschbaren Glieder müssen dabei alle Variationen von Gelenkanzahlen generiert werden, für die vertauschbaren alle Kombinationen. Als Kombinationen wähle ich diejenigen Variationen, bei denen die Gelenkanzahlen der Glieder mit zunehmender Gliednummer nicht größer werden. Wird die Summe der Gelenkanzahlen aller Glieder gebildet, so wird jedes Gelenk genau zweimal gezählt, da es an genau zwei Gliedern beteiligt ist. Die Summe beträgt also immer genau 2k.
Achtgliedrige Mechanismen, 2k = 20.
Es sind folgende Gelenkverteilungen theoretisch möglich (die Zahlen geben die Gelenkanzahlen der Glieder 0 bis 7 an, die Glieder 0 und 1 sind Gestell und Antrieb):
| 6-2-2-2-2-2-2-2 | 5-3-2-2-2-2-2-2 | 5-2-3-2-2-2-2-2 | 4-4-2-2-2-2-2-2 |
| 4-3-3-2-2-2-2-2 | 4-2-4-2-2-2-2-2 | 4-2-3-3-2-2-2-2 | 3-5-2-2-2-2-2-2 |
| 3-4-3-2-2-2-2-2 | 3-3-4-2-2-2-2-2 | 3-3-3-3-2-2-2-2 | 3-2-5-2-2-2-2-2 |
| 3-2-4-3-2-2-2-2 | 3-2-3-3-3-2-2-2 | 2-6-2-2-2-2-2-2 | 2-5-3-2-2-2-2-2 |
| 2-4-4-2-2-2-2-2 | 2-4-3-3-2-2-2-2 | 2-3-5-2-2-2-2-2 | 2-3-4-3-2-2-2-2 |
| 2-3-3-3-3-2-2-2 | 2-2-6-2-2-2-2-2 | 2-2-5-3-2-2-2-2 | 2-2-4-4-2-2-2-2 |
| 2-2-4-3-3-2-2-2 | 2-2-3-3-3-3-2-2 |
Gegenüber dem Basisalgorithmus verringert sich so die Anzahl der untersuchten Gelenkverteilungen von 7149 auf 26.
Wie bereits angesprochen, können verschiedene Gelenkmengen durchaus denselben Typ besitzen. Jeder Typ steht also für eine Menge von Gelenkmengen, wobei die Eindeutigkeit eines Typs für verschiedene Typen disjunkte Mengen verlangt. Beim Basisalgorithmus wird eine gefundene Gelenkmenge mit allen Elementen der durch alle Typen gebildeten Mengen verglichen. Die Anzahl der Vergleiche ließe sich erheblich reduzieren, wenn zuerst die durch den Typ gebildete Menge der neuen Gelenkmenge ermittelt und diese dann nur noch mit den kompletten Mengen der bereits gefundenen Typen verglichen würde. Dafür ist eine Identifikation der Mengen erforderlich - sozusagen ein echter Typencode. Da die Mengen disjunkt sind, können sie durch jeweils einen Repräsentanten eindeutig gekennzeichnet werden. Wichtig ist dabei nur, daß stets der gleiche Repräsentant gewählt wird - am einfachsten ein extremales Element. Selbst wenn zum Finden dieses extremalen Elementes alle n! Permutationen der neuen Gelenkmenge getestet werden müssen, verringert sich die Anzahl der Vergleiche gegenüber dem Basisalgorithmus von N2*(n-s)!*M/2 auf N2*(n-s)! zum ermitteln des Typencodes plus durchschnittlich N2*M/2 zum Vergleich mit den vorhandenen Typen, die ebenfalls als Typencode gespeichert sind. [Anm.: N2 ist die Anzahl der Schleifendurchläufe, in denen der Test in Zeile 2 des Basisalgorithmus positiv ausfällt.]
Im Folgenden beschreibe ich nun ein Verfahren, mit dem sich ein extremales Element der aus einer gegebenen Gelenkmenge durch Permutation der Glieder entstehenden Menge mittels Prüfen von nur wenigen statt n! Elementen finden läßt. Dazu wird folgende Numerierung der prinzipiell möglichen Gelenken zwischen den n Gliedern benutzt: Sind a und b die Nummern der durch das Gelenk verbundenen Glieder mit 0≤a<b sind, so ergibt sich die Nummer des Gelenkes aus a + (b@2). Diese mit 0 beginnende Numerierung ist eindeutig und lückenlos, wie im Anhang bewiesen wird. Extremal soll nun diejenige Darstellung einer Struktur sein, die mit den niedrigsten Gelenken auskommt, wobei der Vergleich beim jeweils höchsten beginnt.
Zuerst wird das Glied gewählt, das die höchste Nummer (n-1) erhalten soll. Die Gelenke dieses Gliedes sich die mit den höchsten Nummern und haben daher den größten Einfluß auf die Einordnung der Darstellung. Da nur die Darstellung mit den kleinsten Gliednummern gefragt ist, müssen nur die Glieder für die höchste Nummer in Betracht gezogen werden, die hier die geringsten Gelenknummern zulassen. Die mit dem gewählten Glied verbundenen Glieder werden automatisch auf die niedrigsten Nummern gelegt, aber eine konkrete Zuordnung kann noch nicht erfolgen. Stattdessen erfolgt eine Aufteilung der Glieder in Gruppen, deren Elemente später Nummern in einem zusammenhängenden Bereich belegen werden.
Die Zuordnung der Gliednummern wird immer bei der (echten) Gruppe mit den höchsten vorgemerkten Nummern fortgesetzt, denn diese sind jetzt entscheidend für die Extremalität. Hier gestaltet sich der Vergleich etwas komplizierter, da die Zugehörigkeit der verbundenen Glieder zu den bereits bestehenden Gruppen berücksichtigt werden muß. Neben seiner eigenen Gruppe (der mit den höchsten Nummern) können durch die Entscheidung für ein Glied auch weitere Gruppen aufgespalten werden, wenn diese nämlich mit dem gewählten Glied verbundene Glieder enthalten. Insgesamt kommt es nur selten vor, daß mehrere Varianten verfolgt werden müssen. Sobald alle Gruppen aufgeteilt sind, kann die nun vollständige Darstellung in die Suche nach dem Extremum einbezogen werden.
Ein achtgliedriger Mechanismus.
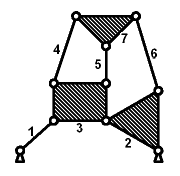
Die Glieder 0 und 1 (Gestell und Antrieb) sind nicht vertauschbar. Den restlichen Gliedern können die Nummern 2 bis 7 zugeteilt werden.
Gruppen vor der Wahl von Glied 7: 0 → 0; 1 → 1; 2, 3, 4, 5, 6, 7 → 2..7
Die Nummern der Gelenke bei Glied 7 ergeben sich aus (7@2) +Gliednummer.
Möglichkeiten der Wahl von Glied 7:
| Glied | verbundene Glieder | Gruppen der verbundenen Glieder | minimale mögliche Gelenknummern bei Glied 7 |
| 2 | 0, 3, 6 | 0, 2..7, 2..7 | 24, 23, 21 |
| 3 | 1, 2, 4, 5 | 1, 2..7, 2..7, 2..7 | 25, 24, 23, 22 |
| 4 | 3, 7 | 2..7, 2..7 | 24, 23 |
| 5 | 3, 7 | 2..7, 2..7 | 24, 23 |
| 6 | 2, 7 | 2..7, 2..7 | 24, 23 |
| 7 | 4, 5, 6 | 2..7, 2..7, 2..7 | 25, 24, 23 |
Als Glied 7 kann nur eins der Glieder aus den gefärbten Zeilen gewählt werden, um eine extremale Codierung zu erreichen. Es müssen also drei Fälle untersucht werden.
Fall 1: 4 → 7
Um die gewünschten Gelenknummern 24 und 23 bei Glied 7 zu erreichen, müssen die Glieder 3 und 7 die Nummern 2 und 3 erhalten - eine neue Gruppe ensteht.
Gruppen vor der Wahl von Glied 6: 0 → 0; 1 → 1; 3, 7 → 2..3; 2, 5, 6 → 4..6; 4 → 7
| Glied | verbundene Glieder | Gruppen der verbundenen Glieder | minimale mögliche Gelenknummern bei Glied 6 |
| 2 | 0, 3, 6 | 0, 2..3, 4..6 | 19, 17, 15 |
| 5 | 3, 7 | 2..3, 2..3 | 18, 17 |
| 6 | 2, 7 | 4..6, 2..3 | 19, 17 |
Die Zuordnung ist eindeutig: 5 → 6.
Gruppen vor der Wahl von Glied 5: 0 → 0; 1 → 1; 3, 7 → 2..3; 2, 6 → 4..5; 5 → 6; 4 → 7
| Glied | verbundene Glieder | Gruppen der verbundenen Glieder | minimale mögliche Gelenknummern bei Glied 5 |
| 2 | 0, 3, 6 | 0, 2..3, 4..5 | 14, 12, 10 |
| 6 | 2, 7 | 4..5, 2..3 | 14, 12 |
Die Zuordnung ist wiederum eindeutig: 6 → 5.
Nun sind alle Gruppen aufgespalten, d.h. die Zuordnung aller Gliednummern steht für Fall 1 fest:
0 → 0; 1 → 1; 7 → 2; 3 → 3; 2 → 4; 6 → 5; 5 → 6; 4 → 7
Das ergibt die Gelenknummern 24, 23, 18, 17, 14, 12, 9, 6, 4, 0.
Fall 2: 5 → 7
Verläuft analog zu Fall 1 und ergibt die gleichen Gelenknummern.
Fall 3: 6 → 7
Gruppen vor der Wahl von Glied 6: 0 → 0; 1 → 1; 2, 7 → 2..3; 3, 4, 5 → 4..6; 6 → 7
| Glied | verbundene Glieder | Gruppen der verbundenen Glieder | minimale mögliche Gelenknummern bei Glied 6 |
| 3 | 1, 2, 4, 5 | 1, 2..3, 4..6, 4..6 | 20, 19, 17, 16 |
| 4 | 3, 7 | 4..6, 2..3 | 19, 17 |
| 5 | 3, 7 | 4..6, 2..3 | 19, 17 |
Fall 3.1: 4 → 6
Alle Gruppen sind aufgespalten:
0 → 0; 1 → 1; 7 → 2; 2 → 3; 3 → 4; 5 → 5; 4 → 6; 6 → 7
Das ergibt die Gelenknummern 24, 23, 19, 17, 14, 12, 9, 7, 3, 0.
Fall 3.2: 5 → 6
Alle Gruppen sind aufgespalten:
0 → 0; 1 → 1; 7 → 2; 2 → 3; 3 → 4; 4 → 5; 5 → 6; 6 → 7
Das ergibt ebenfalls die Gelenknummern 24, 23, 19, 17, 14, 12, 9, 7, 3, 0.
Die gesuchte extremale Gelenkmenge ist offensichtlich die aus den Fällen 1 und 2. Sie ist der Typencode des achtgliedrigen Mechanismus.
Das Beispiel zeigt, daß die Bestimmung des Typencodes schon bei relativ kleinen Strukturen recht aufwendig sein kann. Tatsächlich wird im endgültigen Programm dann auch ein nicht unerheblicher Teil der Laufzeit für die Bestimmung der Codes benötigt. Trotzdem ist diese Methode natürlich um Größenordnungen schneller als eine Bestimmung der extremalen Gelenkmenge durch Prüfen aller Permutationen, womit das gesteckte Ziel nicht erreicht werden könnte.
In dem Beispiel wird auch ein Ansatzpunkt für eine Beschleunigung des Verfahrens sichtbar. Fall 3 könnte bei der Wahl von Glied 6 abgebrochen werden, da keine der Wahlmöglichkeiten so niedrige Gelenknummern liefert, wie zuvor in den Fällen 1 und 2 bei Glied 6 auftraten. Von dieser Abkürzung werde ich im Programm Gebrauch machen.
Formal sind in den Gelenkmengen Nummern im Bereich 0..(n@2)-1 möglich. Die Extremalität der Typencodes macht für diese jedoch eine stärkere Eingrenzung möglich. Da für alle hier betrachteten Strukturen k < 3n/2 gilt, ist die mittlere Anzahl von Gelenken pro Glied 2k/n < 3. Das ist nur möglich, wenn Glieder mit weniger als drei - also mit zwei - Gelenken enthalten sind. Wird im Verfahren ein solches Glied als das mit der höchsten Nummer gewählt, so liefert es die Gelenknummern ((n-1)@2)+s und ((n-1)@2)+s+1, falls es nur mit vertauschbaren Gliedern verbunden ist. Andernfalls sind die Gelenknummern niedriger. Wird ein anderes Glied gewählt, dann nur, weil es noch geringere Gelenknummern zuläßt. Daher werden in den Typencodes nie Gelenke mit Nummern größer als ((n-1)@2)+s+1 auftreten. Bei achtgliedrigen Mechanismen etwa enthalten die Typencodes keine der Nummern 25, 26 und 27.
Im Anhang wird ein Verfahren zum Aufzählen von Kombinationen beschrieben. Dieses kann als mathematische Grundlage für eine Komprimierung der Codes verwendet werden. Die bei der Berechnung eines Codes gewählte extremale Gelenkmenge ist gerade die mit der geringsten Kombinationszahl, sie ist nie größer als:
((((n-1)@2)+s+2)@k)
Die höchsten Typencodes, die in dieser Arbeit auftreten werden, sind daher die der vierzehn- gliedrigen Mechanismen: das theoretische Maximum liegt hier bei (82@19) ≈ 1,97 * 1018.
Durch die Kompression läßt sich das zu bearbeitende und zu speichernde Datenvolumen tatsächlich stark verringern, für achtgliedrige Mechanismen beispielsweise von log256 (2510)=5,8 Byte auf
log256((25@10))=2,7 Byte pro Code.
Beispiel: der Typencode aus dem Beispiel im vorangegangenen Abschnitt
{24, 23, 18, 17, 14, 12, 9, 6, 4, 0} wird komprimiert zu:
(24@10)+(23@9)+(18@8)+(17@7)+(14@6)+(12@5)+(9@4)+(6@3)+(4@2)+(0@1) = 2.845.599
Zur Kompression wurde hier nur der Mengencharakter der Gelenkmenge genutzt. Die zu speichernden Daten besitzen aber weitere Redundanzen, die aus den mechanischen Eigenschaften der Strukturen folgen. Bezieht man dieses Wissen mit ein, ist eine stärkere Kompression (d.h. noch geringere Typencodes) möglich. Zum Beispiel treten gewisse Teilketten mit Sicherheit in jeder Struktur einer bestimmten Art auf. Die Information darüber ist also nicht notwendig und kann bei der Codierung entfallen. Eine derartige zusätzliche Komprimierung der Typencodes ist jedoch aufwendig, abhängig von der Art der betrachteten Strukturen und nicht erforderlich für die Zwecke dieser Arbeit.