Aufzählen von Kombinationen

Bei einer Kombination ohne Wiederholung werden a aus b Objekten (hier repräsentiert durch natürliche Zahlen) ausgewählt: x₁,x₂,...,x_a mit x_i ∈ 0,1,...,b-1 und x_i≠x_j für i≠j. Für diese Auswahl gibt es (b@a) Möglichkeiten. Die Angabe der x_i ist zur Bezeichnung einer Kombination geeignet, aber Vertauschungen und Wiederholungen führen zu doppelten bzw. unzulässigen Identifikationen. Das im Folgenden beschriebene Verfahren ist dagegen völlig frei von Redundanz. Wenn x_i<x_j für alle i<j gilt, dann liefert die Funktion ∑(x_i@i) eine eineindeutige Abbildung in 0 ... (b@a)-1.

Der Nachweis erfolgt mittels vollständiger Induktion. Die Menge der (b@a) Kombinationen von a aus b Objekten läßt sich anhand des Kriteriums, ob die größte Zahl enthalten ist, in zwei Teilmengen unterteilen. Die Kombinationen, die die Zahl b-1 nicht enthalten, sind genau die Kombinationen von b-1 aus a Objekten und belegen nach Induktionsvoraussetzung die Identifikations-Nummern 0 bis ((b-1)@a)-1. Entfernt man aus den Kombinationen der zweiten Teilmenge das größte Element, verbleiben gerade die Kombinationen von a-1 aus b-1 Objekten, die - wieder nach Induktionsvoraussetzung - die Nummern 0 bis ((b-1)@(a-1)) tragen. Durch das größte Element wird die Summe noch um den Wert ((b-1)@a) vergrößert. Die Nummern der zweiten Teilmenge schließen sich demnach genau an die der ersten Teilmenge an, wodurch sich insgesamt eine lückenlose Abbildung ergibt.

Dieses Schema macht zwei Induktionsanfänge notwendig: für 0 aus b und für b aus b. Beide Fälle sind trivial, da jeweils nur eine Kombination (mit der Nummer 0) existiert.

Beweisschema:

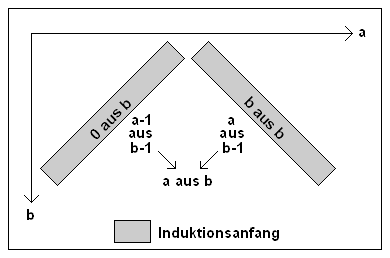
Der Beweis zeigt gleichzeitig eine interessante Eigenschaft der untersuchten Numerierung auf. Da die Kombinationen mit den größeren Objekten stets auch die höheren Identifikationen besitzen, liefert ein Vergleich zweier Nummern des gleiche Ergebnis wie der Vergleich der in den identifizierten Kombinationen enthaltenen Objekte, wobei beim jeweils größten begonnen wird.

Die Eineindeutigkeit der Numerierung stellt nur sicher, daß die Rückgewinnung der Kombination aus der zugehörigen Nummer möglich ist. Es ist aber noch nicht gezeigt, daß dies auch mit praktikablem Aufwand erfolgen kann. Eine vollständige Suche führt in jedem Fall zum Ziel, benötigt aber im Mittel (b@a)/2 Schritte und ist damit für den praktischen Einsatz ungeeignet.

Das Problem läßt sich über folgende Überlegung lösen: Die Kombinationen von a aus b, bei denen alle Zahlen kleiner sind als eine Zahl m, belegen die gleichen Nummern wie die Kombinationen von a aus m - also genau 0 bis (m@a)-1. Davon entfallen auf Kombinationen, die die nun größte mögliche Zahl m-1 nicht enthalten, die Nummern der Kombinationen von a aus m-1, also 0 bis ((m-1)@a)-1. Alle übrigen Nummern, also ((m-1)@a) bis (m@a)-1 gehören zwangsläufig zu Kombinationen, die die Zahl m-1 als größte Zahl enthalten. Mit Hilfe dieses Kriteriums läßt sich die größte in einer Kombination enthaltene Zahl x_a in maximal b Tests feststellen.

Wird der durch diese Zahl gebildete Summand (x_a@a) aus der Summe entfernt, entspricht die Restsumme der Nummer einer Kombination von x_a aus b-1. Daraus läßt sich nun analog die ehemals zweitgrößte, jetzt größte enthaltene Zahl x_a-1 in maximal b-1 Tests ermitteln. Dieses Verfahren kann bis zur Ermittlung der kleinsten Zahl fortgesetzt werden, insgesamt sind dafür maximal b(b+1)/2 Tests erforderlich.